三角関数を学ぶ必要はあるのか
サイン、コサイン、タンジェント。高校数学で学ぶ呪文のようなアレです。三角関数。
あんな難しくてわけのわからないものを学んで、一体何の役に立つのでしょうか。ほとんどの人は、大人になってから三角関数の知識を使ったことなんて一度も無いでしょう。
そんな三角関数、本当に学校で学ぶ必要があるのか?
三角関数とは
三角関数とは、簡単に言うと「角度がわかれば長さが分かる」というものです。
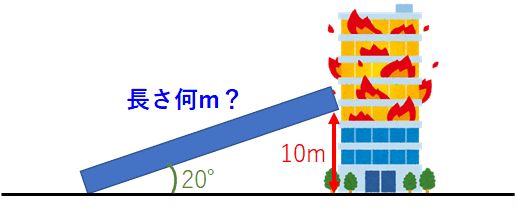
例えば、火災避難用の脱出すべり台を考えてみましょう。このすべり台は角度固定で20°。それを高さ10mの位置に設置するとき、すべり台の長さは何メートル必要か? という話です。答えは、
$$すべり台の長さ=\frac{10\mathrm{m}}{\sin20°}=29.23\mathrm{m}$$
となります。サイン(sin)、コサイン(cos)、タンジェント(tan)のうちどれを使うのか、どのように掛け算とか割り算をするのかはとりあえず置いといて、重要なのは三角関数を使うと角度から長さが計算できるということです。
高校数学の三角関数の難しさ
さっきのすべり台のような実例があればまだとっつきやすいかもしれませんが、高校数学の教科書に載っている三角関数は、
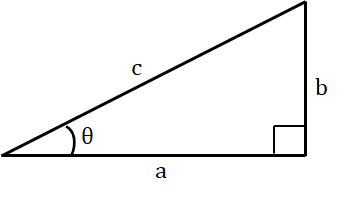
直角三角形において、
$$\sin{\theta}=\frac{b}{c}, \cos{\theta}=\frac{a}{c}, \tan{\theta}=\frac{b}{a}$$
とする。
……ってやつなんですよね。なんだそれ、わけわかんねー。大体、θ(シータ)て何やねん、その形はカプセル錠剤か? 熱・鼻・のどに効くのか?
「直角三角形」などという無機質なモノに対してサインやらコサインやら変な記号がたくさん出てきて、何がしたいのかわからないままに学校の授業は進んでいきます。
学校の先生によっては、初回の授業で「これは角度と長さの関係がわかるものなんだよ。例えばすべり台があってねぇ」と、実例を教えてくれるかもしれません。
そういう余談を挟んでくれればまだわかりやすいかもしれないですが、ほとんどの場合は無機質に授業はどんどん進んでいきます。最初のサインとかコサインとかいう時点ですでにわけがわからないのに、加法定理とか余弦定理とか、ますますわからないのがどんどん出てきます。
$$余弦定理:a^2=b^2+c^2-2bc\cos{A}$$
$$加法定理:\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}$$
こんなん覚えられるか! っていうか、これを覚えて何が楽しいねん!
しかも、生れ落ちて15年、角度ってやつは0°~360°だと習ってきたのに、突然ラジアンというのが出てきて、「今日から90°のことを\(\pi/2\)ラジアン≒1.57ラジアンと呼びましょう」とか言われて、ふざけんな、そんなの聞いたことねぇぞ! どこで使うねん! ってなるわけです。
そんなこんなの三角関数。果たして学ぶ必要が本当にあるのか? と思う気持ちもよくわかります。
学校の授業のレベル
そもそも、学校で学ぶ授業のレベルってどんなものなんでしょうか。科目によって多少の違いはあると思いますが、僕は大体このようなものだと思っています。
- 小学校 -- 日常生活に困らないだけの知識を学ぶ
- 中学校 -- 日常生活をより便利に過ごすための高度な知識を学ぶ
- 高校 -- 各分野の専門職に就くための知識を学ぶ
- 大学 -- 各分野の学問を究める研究者となるための知識を学ぶ
要するに、中学校の授業の時点で、日常生活を送る上では相当高度な知識を学んでいるわけです。ましてや、高校の授業なんてものは、何らかの専門職にでも就かない限り、全く日常生活においては必要ではありません。大学の授業で学ぶ知識に至っては、専門職ですら必要無いくらいです。
つまり、高校数学で学ぶ三角関数も、よほどの理学や工学の専門職に就かないのであれば、日常生活では全く必要ありません。
でも、逆に言えば、そのような専門職に就くつもりなら、三角関数くらいはわかっていないと厳しいかもしれません。
はい、答えは出ました。「三角関数を学ぶ必要はあるのか?」という問いに対しては、「必要の無い人にとっては必要が無い、必要のある人にとっては必要がある」というのが答えです。
……って、これじゃぁミもフタも無い答えですね。
三角関数を知らなくてもいいのか
ある人(仮名:瀬戸内さん)がこんなことを言っていました。

三角関数を学ぶ必要なんて無い。それが必要になったらどうするかって? そのときは専門の人を雇って計算させればいい。
確かに、専門的な高度な知識というのは専門家に任せるべきです。専門家にお金を払うことによって物事がスムーズに進むのなら、それは良い選択だと思います。
しかしここで、別の人(仮名:王華さん)の例を見てみましょう。その人は、舞台などでパフォーマンスを演じるパフォーマー。あるとき、舞台全体を明るく照らすための照明をどうすればいいか、という問題に直面しました。
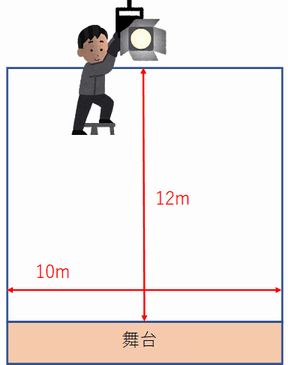

舞台の幅が10メートルで、後ろの照明から舞台までが12メートル。照明で舞台全体を照らしたいんだけど、照明の角度(広さ)はどれくらい必要なのかな?
王華さんは簡単なイラストを用意して、この問いをtwitterに投げかけました。答えから言えば、
$$照明の角度=2×\tan^{-1}\frac{5}{12}=約45.24°$$
となります。おそらく、照明器具の羽の部分をどう調節すればいいか、あるいはどのタイプの照明器具を買えば舞台全体を照らすことができるのかを知りたかったのでしょう。
王華さんは工学の専門職ではありません。\(\tan^{-1}\)という逆正接関数(アークタンジェント)を使えば計算できる…ということはわからなかったのでしょう。しかし、頭の片隅に三角関数の知識があったはずです。サインだかコサインだかは忘れたけど、確か、長さから角度を計算することができるよね? と。
そしてさらに、その計算方法は、自分にはわからないけども現役高校生や大学生ならわかるはずだ、というカンが働き、twitterで聞けば誰かが答えてくれるはずだ、という予想を立てることができたのです。その思惑通り、数人の人が電卓で計算して王華さんに教えてあげました。
この王華さんは、たとえ自分の頭の中から三角関数のことは消え失せてしまっていたとしても、「それを学ぶことには一定の意義がある」という価値観が心の中にあったからこそ、このように迅速に答えに辿りつけたのでしょう。
一方、先ほどの瀬戸内さんの例はどうでしょうか。このような三角関数の問題が、実はそれほどの専門職の人を雇わなくても現役高校生や大学生なら計算できる、ということにすら思いが至っていません。学ぶことを放棄して、全てを金で解決しようとしています。
その結果、無駄な費用を支払うことになるでしょう。この瀬戸内さんはおそらく、数学だけでなくあらゆる「ちょっとした専門知識」を知るために、その都度高額な費用を払い続けることになります。ほんの少しだけ頭の片隅に「昔学校で学んだ知識」が残っていれば、それが高額な費用を払ってまで得るような知識かどうかの判断が付きそうなものを。
学ぶ必要があるか、と問うこと自体が愚問
三角関数を学ぶ必要があるかと問われれば、さっきの繰り返しになりますが、「必要の無い人にとっては必要が無い、必要のある人にとっては必要がある」 というのが答えになります。そんなことは、聞く前からわかっているはずです。
なのに、さっきの例の瀬戸内さんのように「学ぶ必要が無い」と言い切ったり、「学ぶ必要があるのか?」と問うたりするのは何故なんでしょうか?
それはズバリ、学校教育へのある種の恨みに起因していると思います。あんなわけのわからない三角関数などを勉強させられて、それがわからないと「落ちこぼれ」のレッテルを貼られ、そのせいでさんざんな学校生活だった。大人になった今、ハッキリとその学校教育に仕返しをしてやろう、「こんなものに意味は無い」と喝破することによってね!
……その心の声が文脈の中からにじみ出ているのがバレバレなので、僕はいつも「学ぶ必要があるか」という問いについては軽く流しています。ああ、この人は学校教育に恨みがある人なんだな、と。
然り。さっきも言ったように、高校で学ぶ授業の大部分は、日常生活にとっては不要です。しかし、たかが15歳かそこらの子供に、何が必要で何が不要かなど、判断できるでしょうか?
高校というところは、あらゆる分野の専門職に必要な極めて高度な知識を学ぶ場所です。人間、全分野に精通している必要は無いので、いずれそのうちいくつかは不要になるでしょう。
しかし、学んでおいて損はありません。大人になってから、「やっぱり必要無かったな」と思っても、それでもいいじゃないか。子供だった当時はその判断が付かなかったのだから。
そして、不要だったと思われた知識もどこか頭の片隅には残っているものです。それがいつどんなときに自分にとって利をもたらすかはわかりません。あのときの勉強がほんの少しでも役に立てばラッキーじゃないですか。
勉強を無駄だったと恨み言を言うか、少しでも頭の中に残っていることをラッキーと思うか。どちらが人の心を豊かにすると思いますか?
電卓ブロガー
せっかくなので、さっきの照明の計算を電卓でしてみましょう。
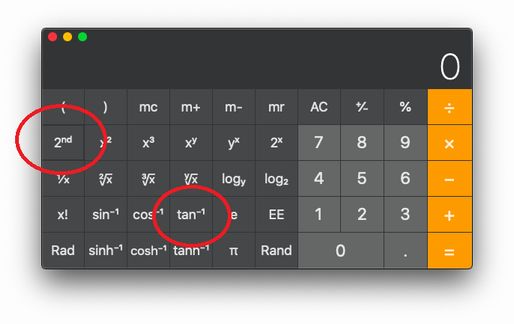
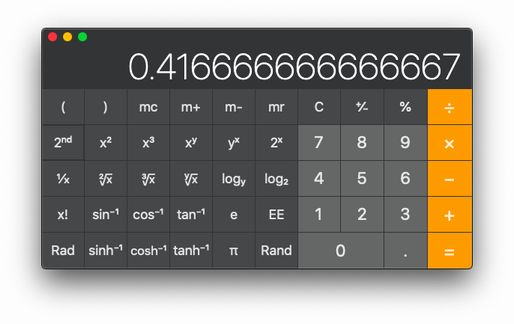
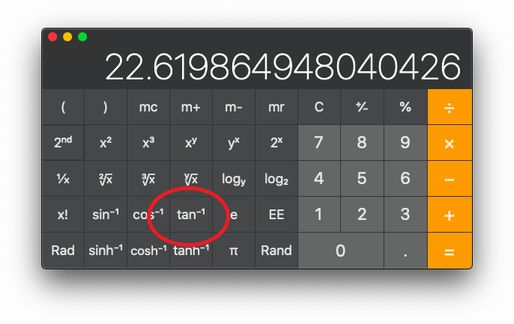

ね、簡単でしょう? こんなのに人を雇ってたら、無駄もいいとこですよ。
これで僕も電卓ブロガーの仲間入り。







ディスカッション
コメント一覧
まだ、コメントがありません